box plot for non normal distribution If I plot some data in function of a categorical variable in R, I get the standard boxplot. However, the boxplot displays non-parametric statistics (quantiles) that don't seem appropriate for normally distributed data. Each junction box is rated by amps to protect you, the circuit, and the junction box. It is critical to have the box with the proper amp ratings. For example, a radial circuit needs a 30 amp box, while a lightning circuit needs a 20 amp box.
0 · skewed to the right boxplot
1 · positively skewed distribution box plot
2 · positively skewed box plots
3 · positive skew vs negative boxplot
4 · how to interpret boxplot results
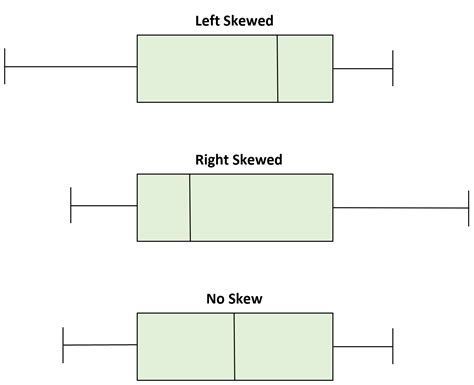
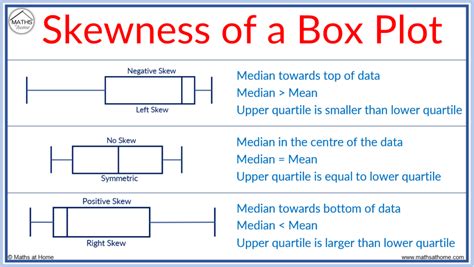
5 · boxplot skewed to the left
6 · box and whiskers chart explained
7 · 25th percentile on a boxplot
What is a CNC Router? Today's desktop CNC routers can accurately cut multiple parts and can cut decorative carving. The new smaller machines are also much more affordable than their industrial big brothers. .
If I plot some data in function of a categorical variable in R, I get the standard boxplot. However, the boxplot displays non-parametric statistics (quantiles) that don't seem appropriate for normally distributed data.
The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank . The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank Harrell suggests. However, I don't think a rug plot will be very enlightening, because of the sheer concentration of 83% of your data points in .
You require an assumed distribution in order to be able to classify something as lying outside the range of expected values. Even if you do assume a normal distribution, declaring data points . Is it the best way to summarize a non-normal distribution? Probably not. Below is a skewed distribution shown as a histogram and a boxplot. You can see the median value of the .
Departures from a normal distribution alter the appearance of the box plot. To illustrate this, we show frequency distributions and descriptive statistics in Table 2, histograms in Figure 3, and .Like reliability analysis, you can use a non-normal distribution to calculate process capability, or alter-natively, you can try to transform your data to follow a normal distribution using either the . Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots show the five-number summary of a set of data: including the minimum .One simple method is with a QQ plot. To do this, use 'qqplot (X)' where X is your data sample. If the result is approximately a straight line, the sample is normal. If the result is not a straight line, the sample is not normal. For example if X = .
Create a box plot for the data from each variable and decide, based on that box plot, whether the distribution of values is normal, skewed to the left, or skewed to the right, and estimate the value of the mean in relation to the median.
If I plot some data in function of a categorical variable in R, I get the standard boxplot. However, the boxplot displays non-parametric statistics (quantiles) that don't seem appropriate for normally distributed data. The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank Harrell suggests. However, I don't think a rug plot will be very enlightening, because of the sheer concentration of 83% of your data points in the interval $[101,428; 101,436]$.You require an assumed distribution in order to be able to classify something as lying outside the range of expected values. Even if you do assume a normal distribution, declaring data points as outliers is a fraught business.
Is it the best way to summarize a non-normal distribution? Probably not. Below is a skewed distribution shown as a histogram and a boxplot. You can see the median value of the boxplot is accurate and the quartile markers (the edges of the 'box') show the skew. The outliers also indicate a skew.
A box plot, sometimes called a box and whisker plot, provides a snapshot of your continuous variable’s distribution. They particularly excel at comparing the distributions of groups within your dataset.Departures from a normal distribution alter the appearance of the box plot. To illustrate this, we show frequency distributions and descriptive statistics in Table 2, histograms in Figure 3, and box plots in Figure 4. We are going to look at four examples of non-normal distributions: (A) skewed, (B) peaked, (C) flat, and (D) bimodal.Like reliability analysis, you can use a non-normal distribution to calculate process capability, or alter-natively, you can try to transform your data to follow a normal distribution using either the Box-Cox or Johnson transformation. When you transform your data, you modify the original data using a function of a variable. Functions Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots show the five-number summary of a set of data: including the minimum score, first (lower) quartile, median, third (upper) quartile, and maximum score.
One simple method is with a QQ plot. To do this, use 'qqplot (X)' where X is your data sample. If the result is approximately a straight line, the sample is normal. If the result is not a straight line, the sample is not normal. For example if X = exprnd(3,1000,1) as above, the sample is non-normal and the qqplot is very non-linear:Create a box plot for the data from each variable and decide, based on that box plot, whether the distribution of values is normal, skewed to the left, or skewed to the right, and estimate the value of the mean in relation to the median.If I plot some data in function of a categorical variable in R, I get the standard boxplot. However, the boxplot displays non-parametric statistics (quantiles) that don't seem appropriate for normally distributed data.
mountain house exterior painted metal roof
The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank Harrell suggests. However, I don't think a rug plot will be very enlightening, because of the sheer concentration of 83% of your data points in the interval $[101,428; 101,436]$.You require an assumed distribution in order to be able to classify something as lying outside the range of expected values. Even if you do assume a normal distribution, declaring data points as outliers is a fraught business. Is it the best way to summarize a non-normal distribution? Probably not. Below is a skewed distribution shown as a histogram and a boxplot. You can see the median value of the boxplot is accurate and the quartile markers (the edges of the 'box') show the skew. The outliers also indicate a skew.A box plot, sometimes called a box and whisker plot, provides a snapshot of your continuous variable’s distribution. They particularly excel at comparing the distributions of groups within your dataset.
Departures from a normal distribution alter the appearance of the box plot. To illustrate this, we show frequency distributions and descriptive statistics in Table 2, histograms in Figure 3, and box plots in Figure 4. We are going to look at four examples of non-normal distributions: (A) skewed, (B) peaked, (C) flat, and (D) bimodal.Like reliability analysis, you can use a non-normal distribution to calculate process capability, or alter-natively, you can try to transform your data to follow a normal distribution using either the Box-Cox or Johnson transformation. When you transform your data, you modify the original data using a function of a variable. Functions Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots show the five-number summary of a set of data: including the minimum score, first (lower) quartile, median, third (upper) quartile, and maximum score.
One simple method is with a QQ plot. To do this, use 'qqplot (X)' where X is your data sample. If the result is approximately a straight line, the sample is normal. If the result is not a straight line, the sample is not normal. For example if X = exprnd(3,1000,1) as above, the sample is non-normal and the qqplot is very non-linear:
skewed to the right boxplot
I have a 2007 328i N51 engine. I pulled the intake manifold and the wiring harness junction box under the throttle body. Now I'm putting it back together and have a plug left over .
box plot for non normal distribution|how to interpret boxplot results